研究方向

二、主要成果

1、数学跨学科问题解决能力理论结构

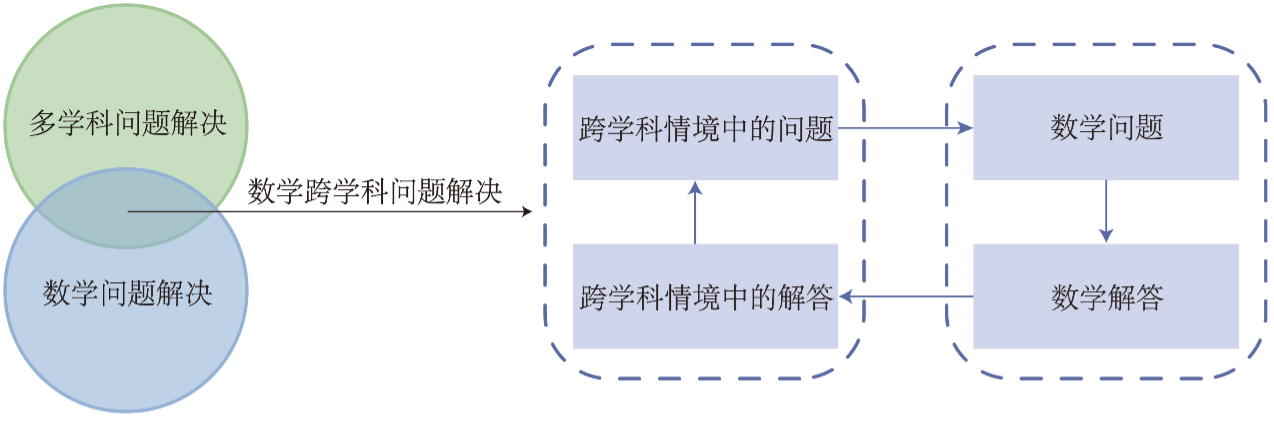
（1）与数学问题解决不同，数学跨学科问题解决以其他学科任务为载体，强调内容的综合性和情境的复杂性。从跨学科情境中的问题出发，学生需要首先识别问题情境与任务，从中抽象出数学问题予以解答，并最终将解答迁移回到原问题情境评估解决效果。这其中既包含常规的良构问题，也包括非常规的劣构问题；

（2）与多学科问题解决不同，数学跨学科问题解决以数学核心素养为导向，强调过程的数学性和思维的逻辑性。学生需要经历数学化的过程，运用数学学科的基础知识、基本方法或基本策略，从而完成问题解决；

（3）重视学生的内在心理因素，这贯穿着数学跨学科问题解决的全过程。

参考文献：

郭衎,杜丙银,姬中天. 指向核心素养的数学跨学科问题解决：测评框架与应用效果[J/OL].中国人民大学教育学刊.

2、数学跨学科问题解决能力测试框架

构建了由问题解决的过程、问题解决的策略、问题解决的态度和问题解决的素养4个一级指标构成的数学跨学科问题解决框架。

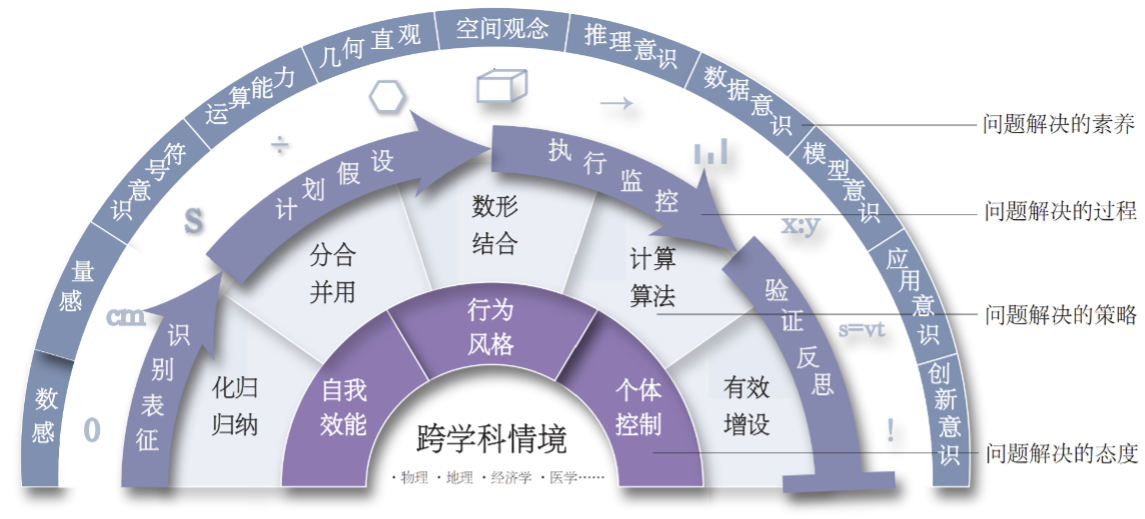
（1）问题解决的过程维度。构建的过程维度的二级指标包括识别表征、计划假设、执行监控和验证反思。

（2）问题解决的策略维度。确立策略维度下的二级指标包括化归归纳、分合并用、数形结合、计算算法和有效增设。

（3）问题解决的态度维度。最终确立态度维度自我效能、行为风格和个体控制三个二级指标。

（4）问题解决的素养维度。该维度体现了主体学科在跨学科问题解决中的重要地位：以其他学科情境为依托，重点对学生体现的（数学）素养水平进行考查和评价。

参考文献：

郭衎,杜丙银,姬中天. 指向核心素养的数学跨学科问题解决：测评框架与应用效果[J/OL].中国人民大学教育学刊.